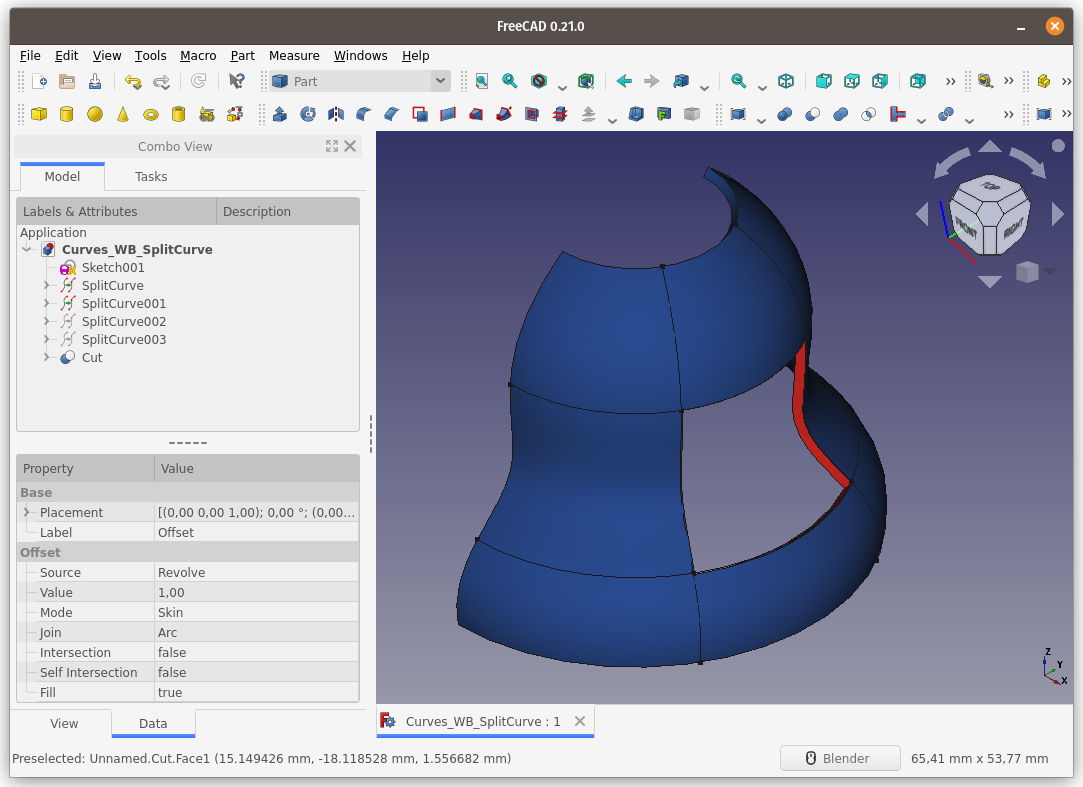
FreeCAD - Curves WB - Curves - 06 - Split curve

Split curve:

Split curve komutu, Seçili eğri(ler)i / kenar(lar)ı parçalara ayırır.

Kullanım: Komutu çalıştırmak için aşağıdaki işlemleri sırasıyla uygulayın:

• Öncelikle, parçalara ayırmak istediğiniz kenarı/eğriyi ya da kenarları/eğrileri seçin.
• Curves araç çubuğunda bulunan ilgili düğmeye basın, ya da
• Curves menüsündeki Split curve seçeneğini kullanın.

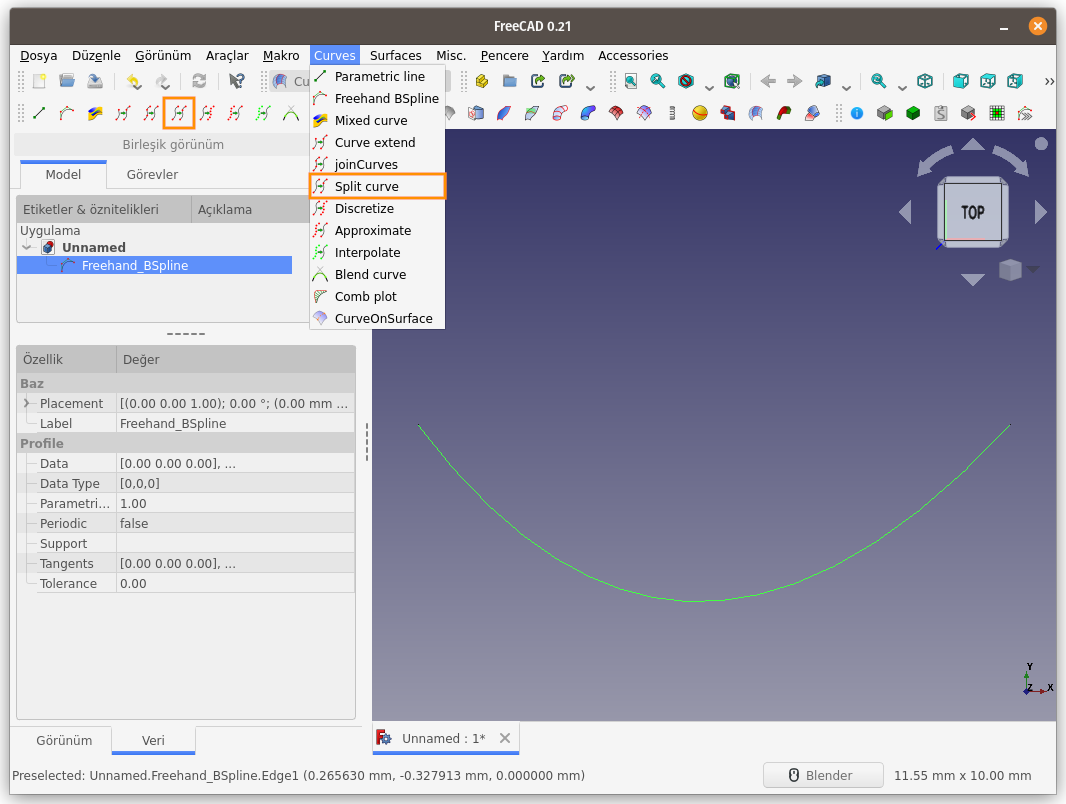
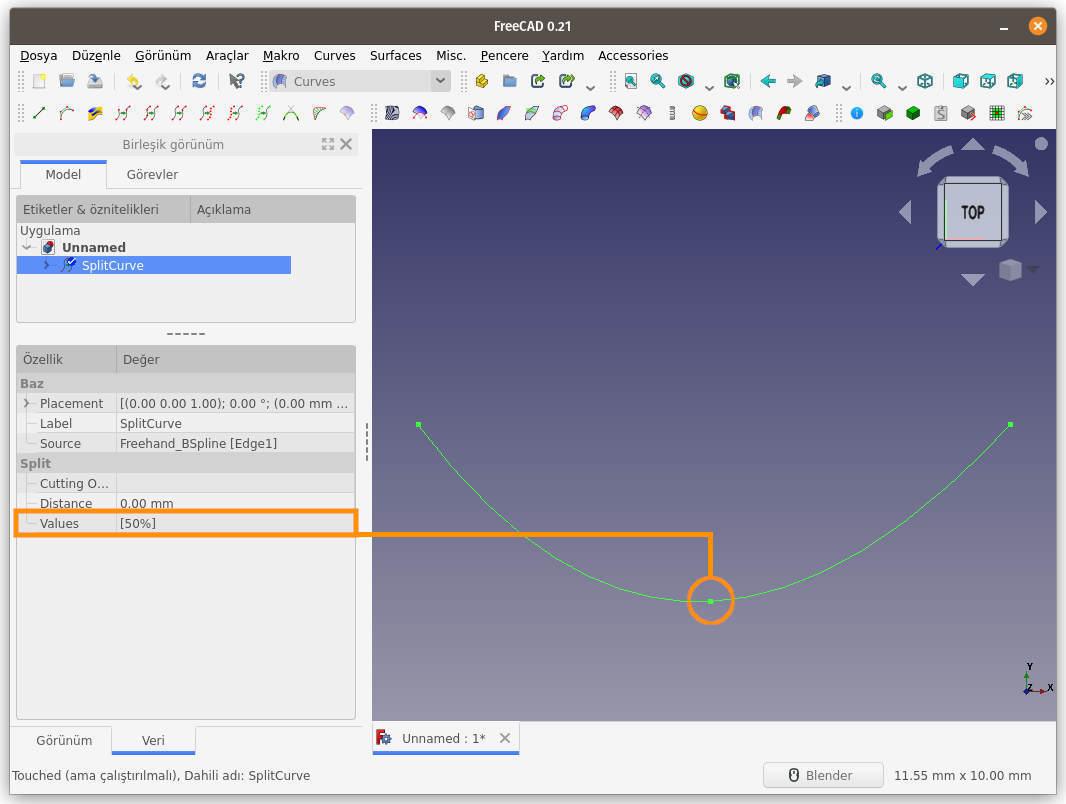
Seçili Eğri, istenilen kısımlardan parçalar ayrılabilir. Kısımlar, komut çalıştırıldıktan sonra Özellikler bölümündeki Veri sekmesinden ayarlanır. Varsayılan değer 50% yani eğrinin tam ortasından bölünmesidir.
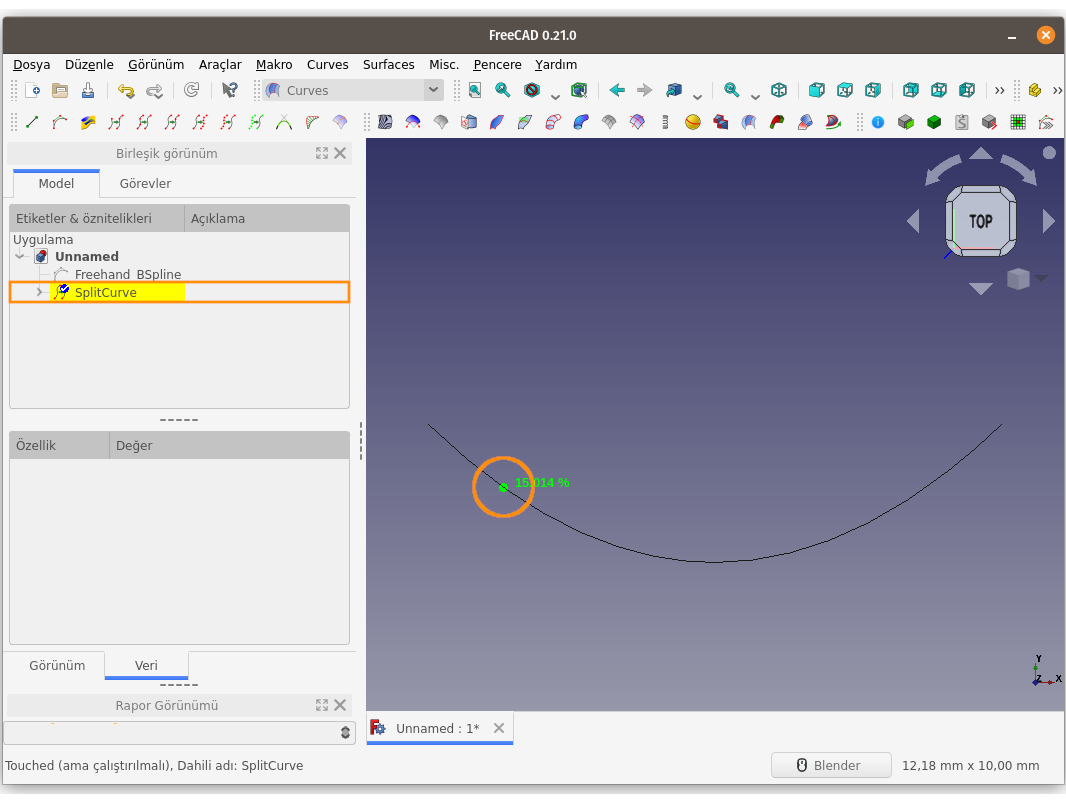
Split curve komutu ile bölünen eğriye, unsur ağacında çift tıklayarak düzenleme moduna girilebilir (düzenleme modunda unsur sarı renkli olarak gösterilir) ve bölüm/ayrım noktası, fare yardımıyla eğri üzerinde hareket ettirerek konumu değiştirilebilir.


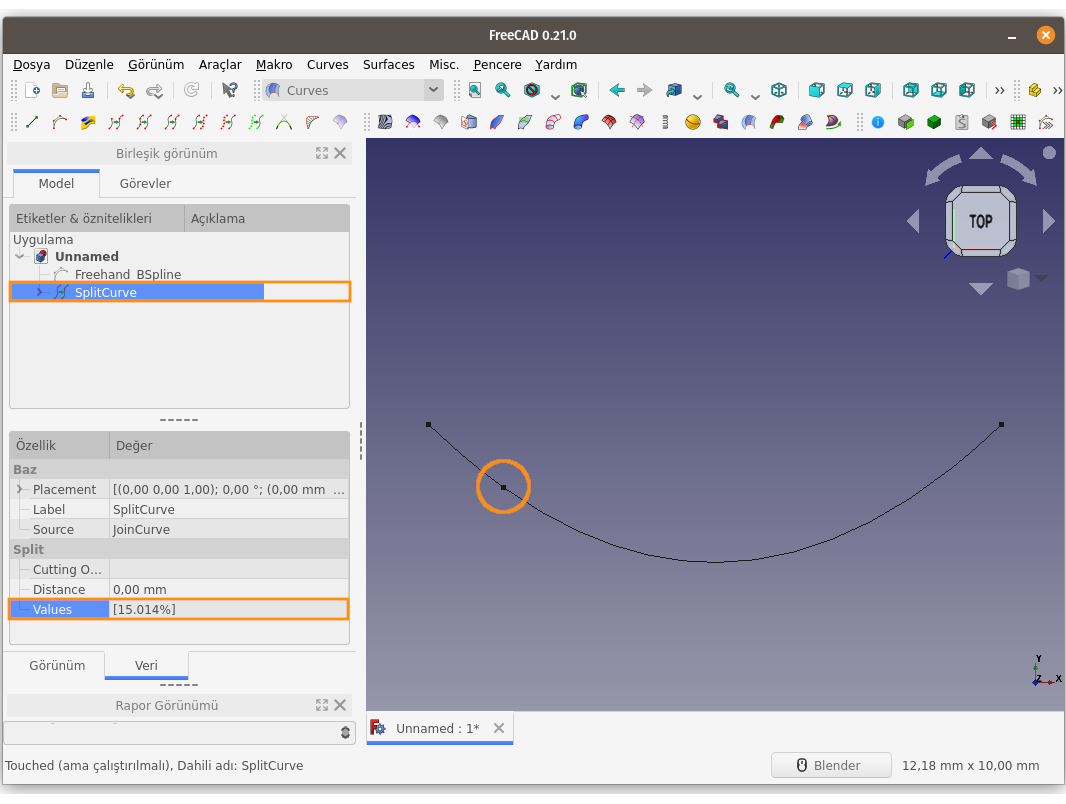
Bölme/Parçalama kısımlarını ayarlamak için başka bir yöntem de, aşağıdaki adımları uygulamaktır;

• Unsur ağacından SplitCurve unsuru seçilir
• Özellikler Panelindeki Split (Böl) başlığı altında bulunan Values (Değerler) İletişim kutusu açılarak her satıra istenilen değerler yazılır.

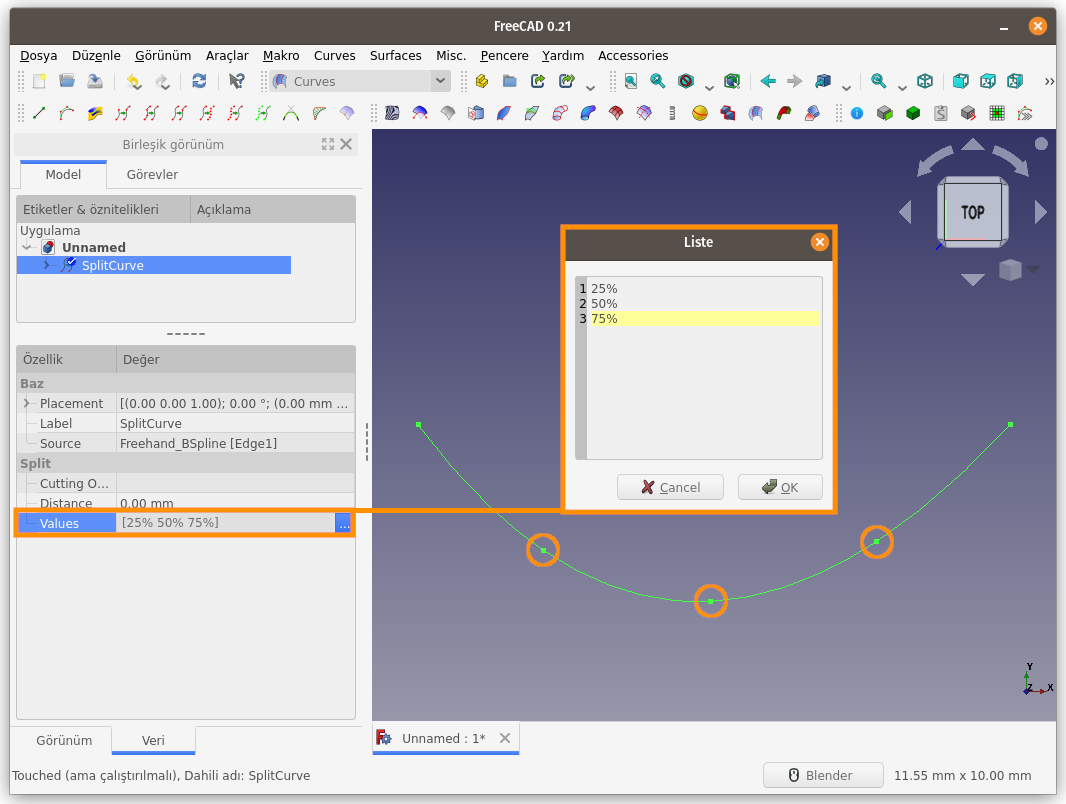
Eğrileri, sayısal değer belirterek parçalara ayırmanın dışında, diğer eğrilerle/kenarlarla kesiştiği noktalardan parçalara ayırmak ta mümkün. Şimdi, 4 eğriyi seçerek, kesişme noktalarından bölmeye/ayırmaya çalışalım.
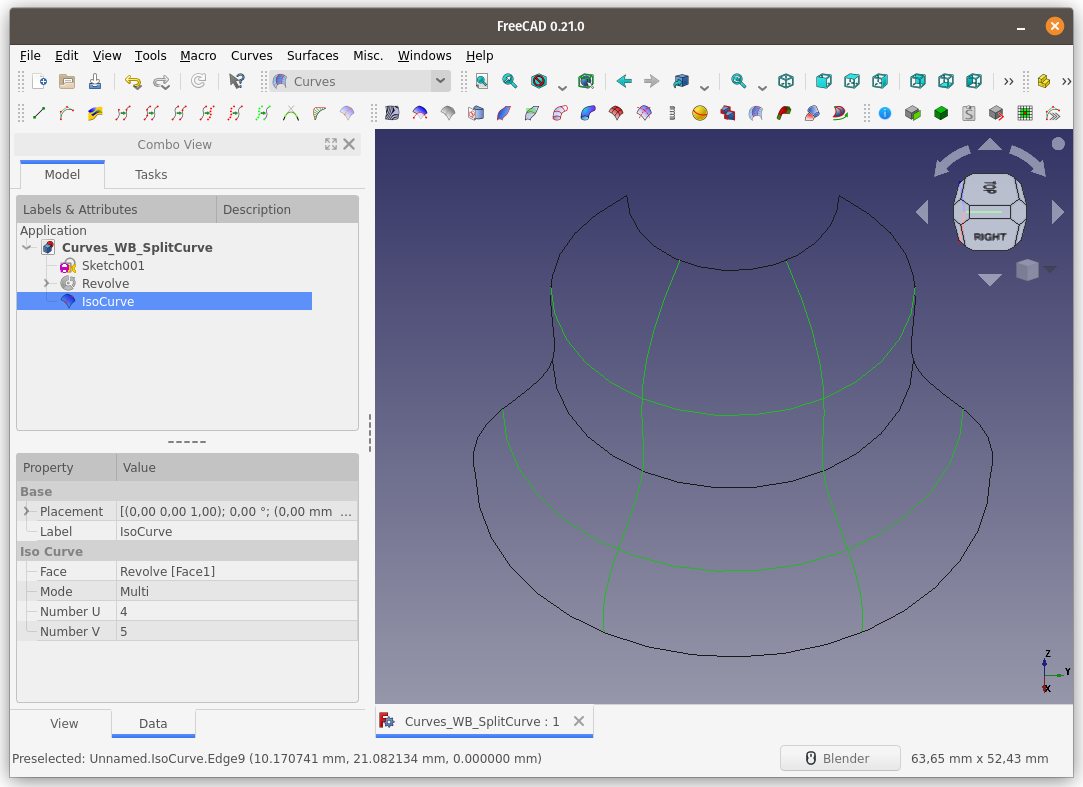
Parçalara ayırmak istediğimiz 4 eğriyi seçtik ve Split curve komutunu çalıştırdık.
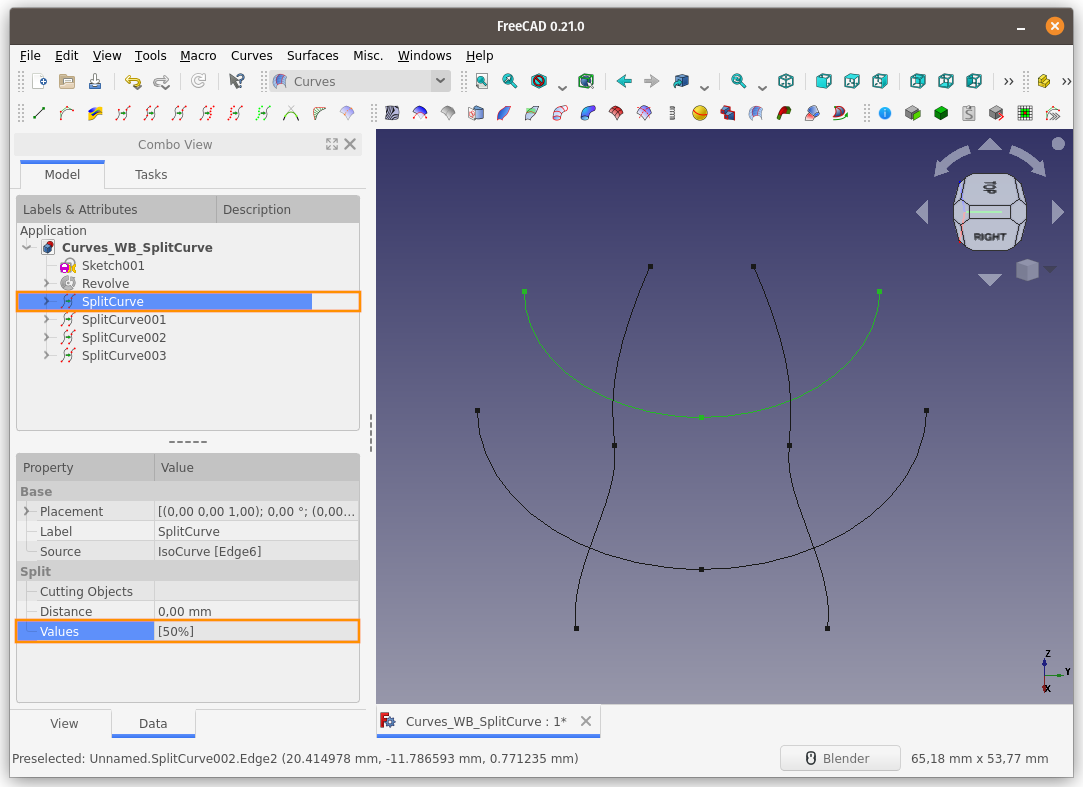
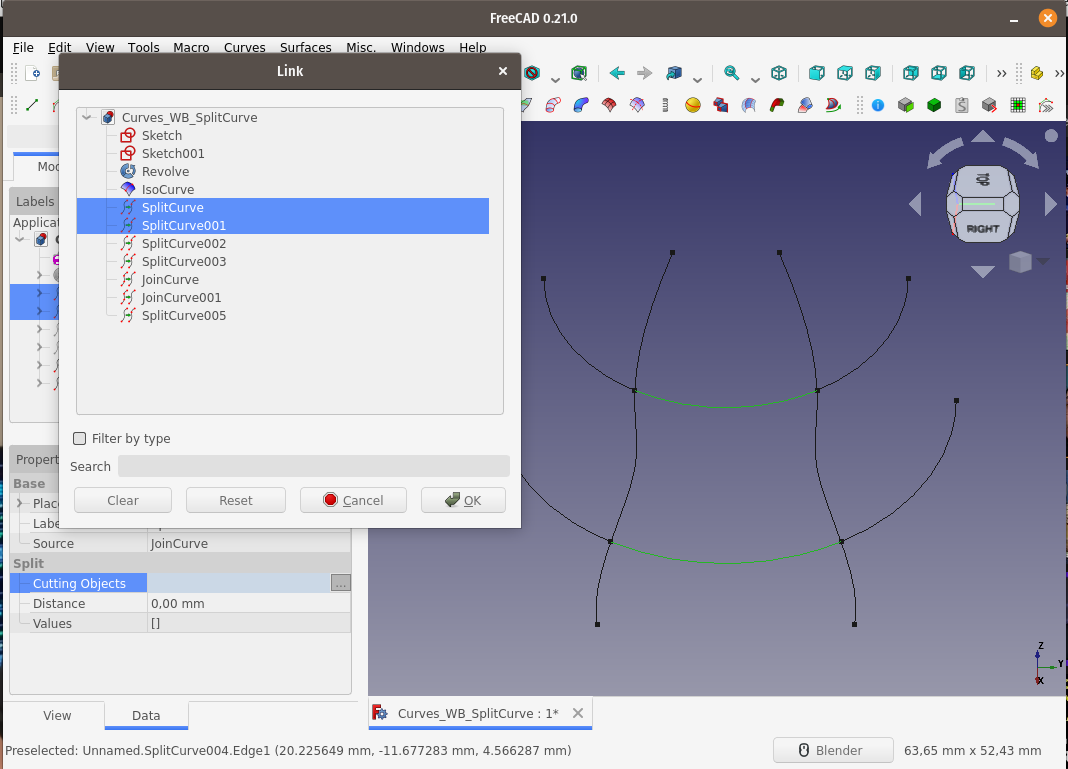
Split curve komutu uygulanan eğrilerden biri seçilir ve Özellikler panelindeki Split başlığı altındaki Values (Değerler) kısmınaki sayısal veriyi silelim (köşeli parantezi silmeyin.) Cutting Objects (Kesim Nesneleri) seçeneğinin sağındaki üç nokta ... butonuna basalım.
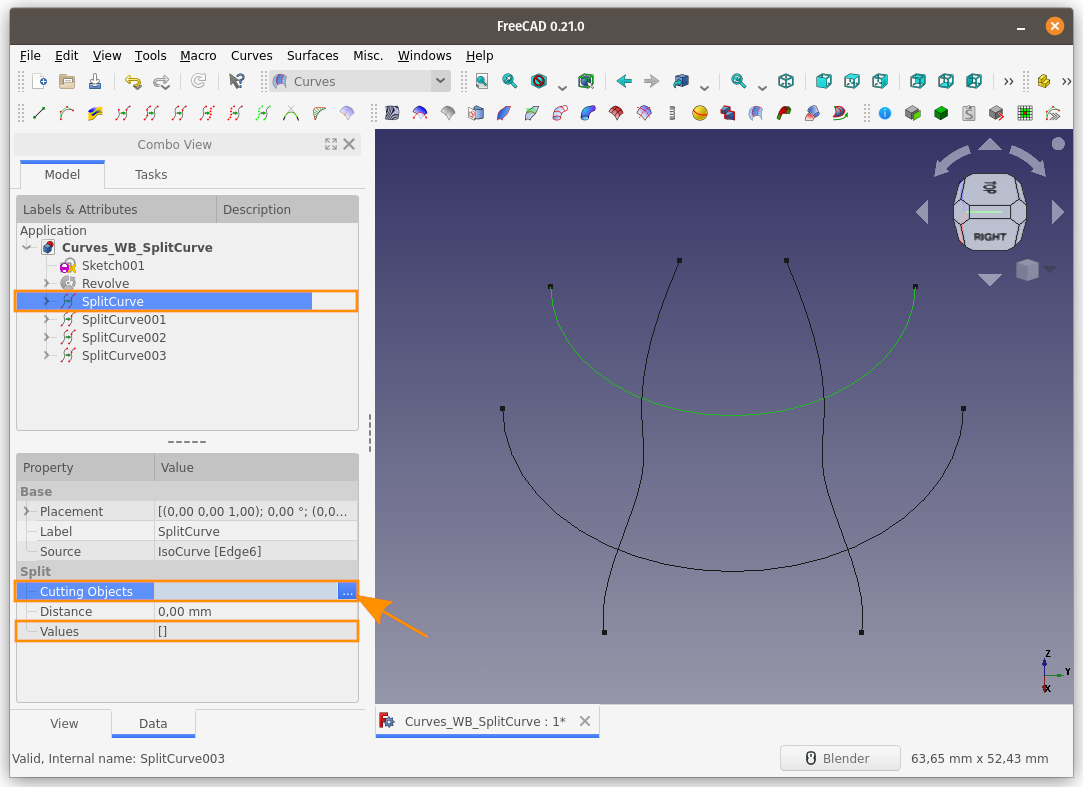
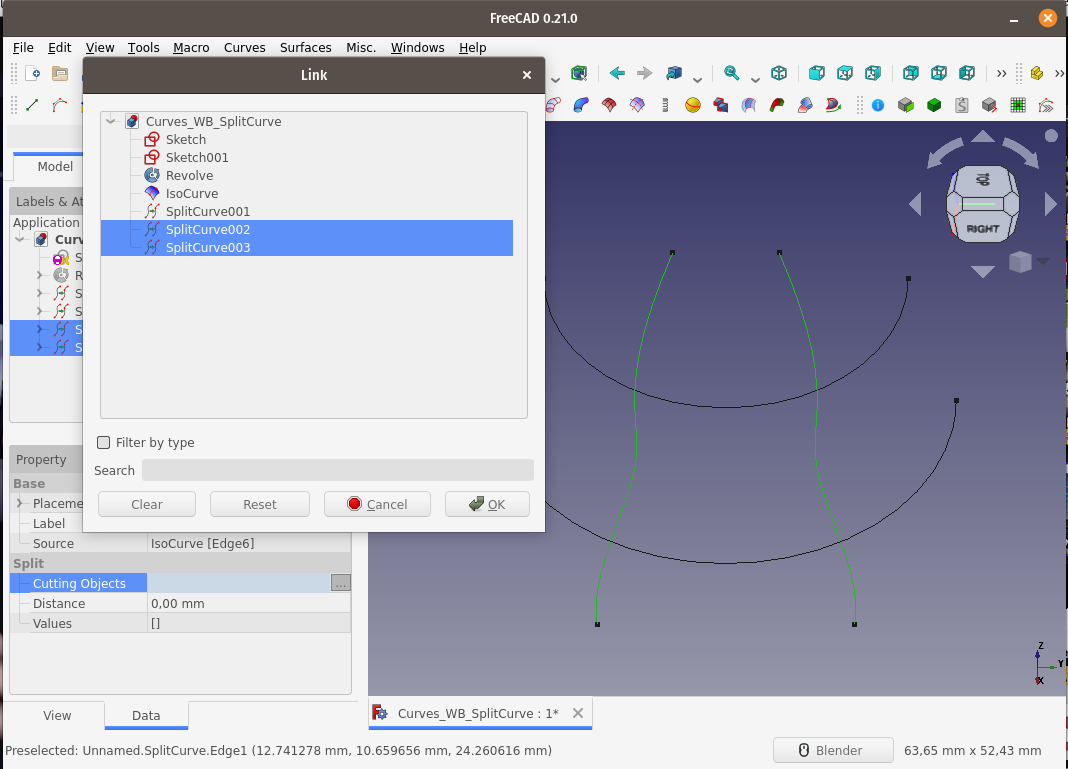
Açılan Link başlıklı diyalog kutusu, Unsur ağacındaki nesneleri görüntüleyecektir. Seçili eğriyi, hangi eğrileri kullanarak bölmek istiyorsak, o eğrileri seçmeliyiz.
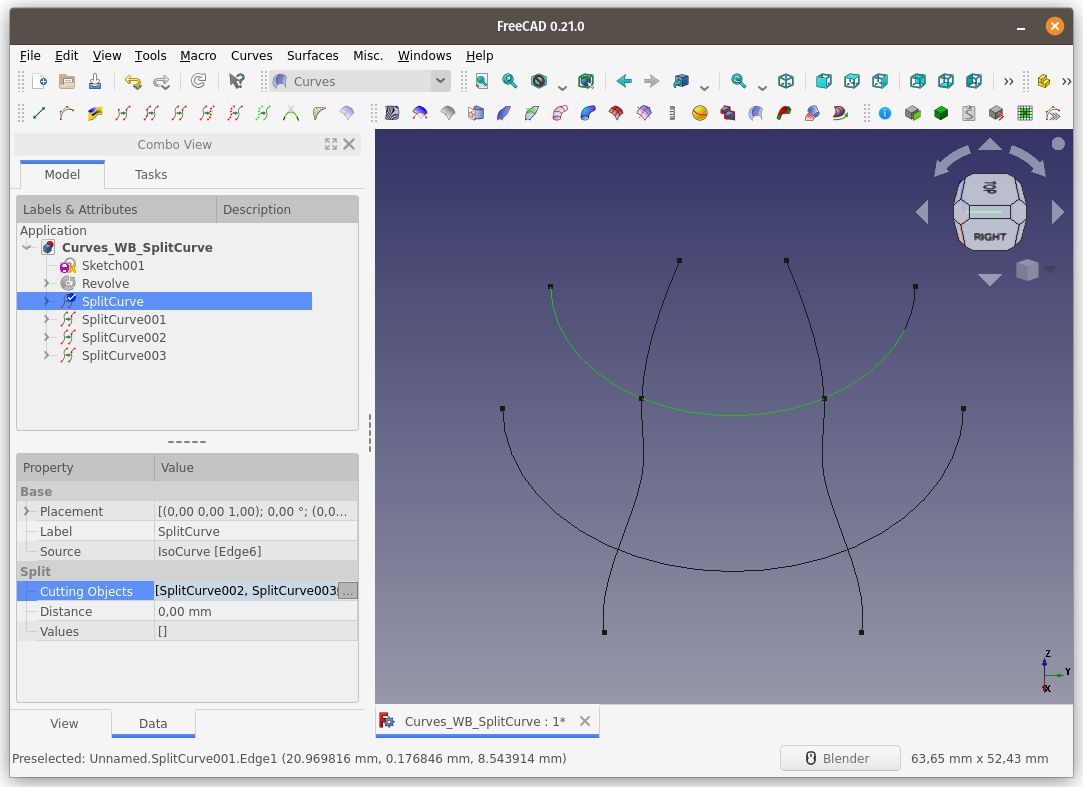
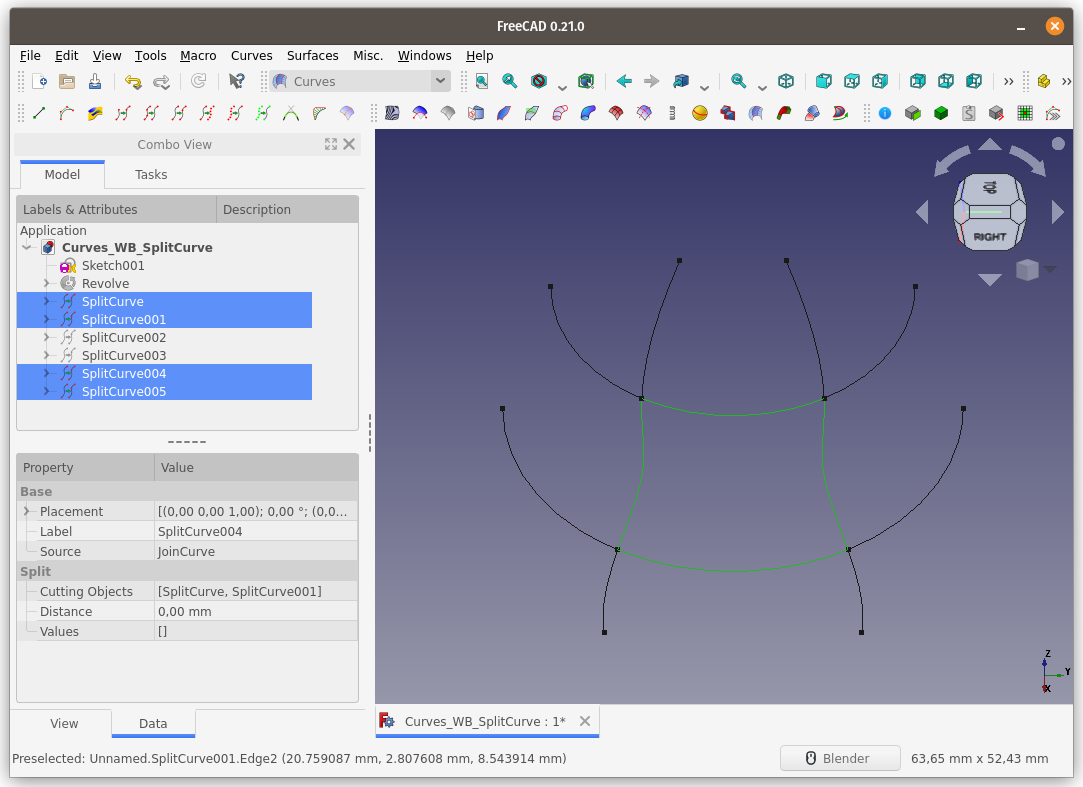
Görüldüğü üzere, eğrimiz, seçili eğrilerle kesişim noktalarından bölündü.
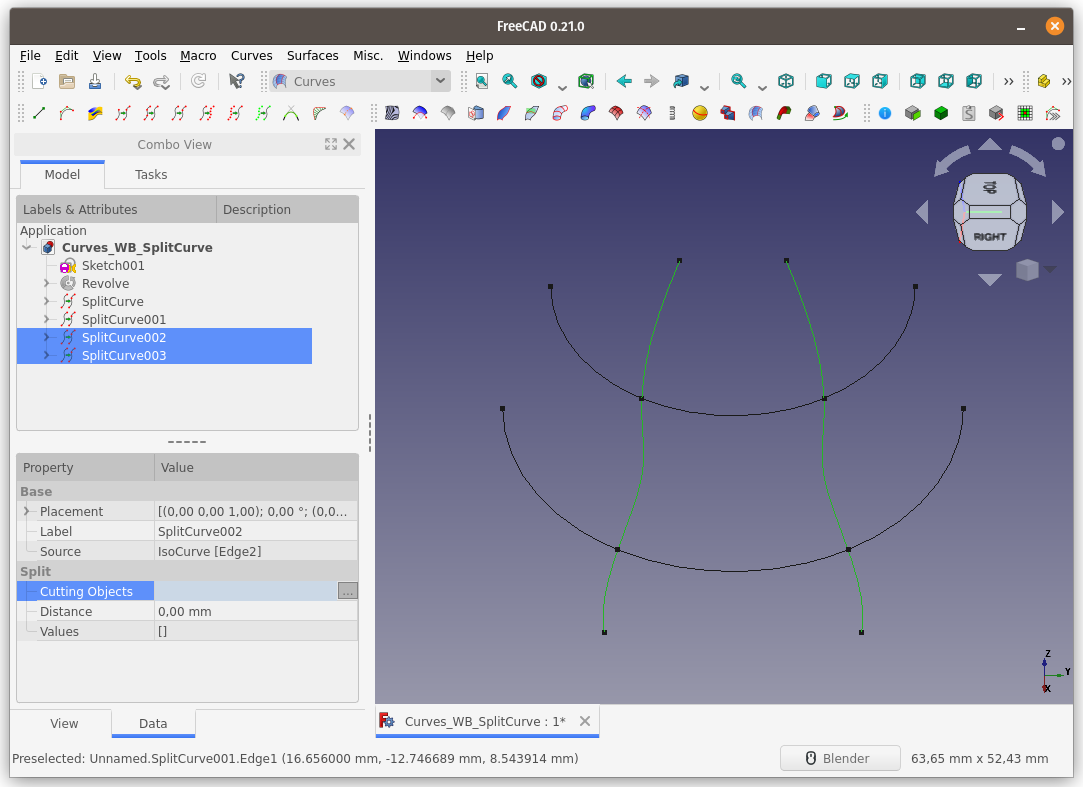
Birden fazla eğriyi aynı anda seçerek, diğer eğrilerle kesişim noktalarından bölmek te mümkün.

Bölünmüş eğriler seçerek bir yüzey oluşturmaya çalışalım.
Oluşan yeni yüzeyi, ana yüzeyden çıkaralım.
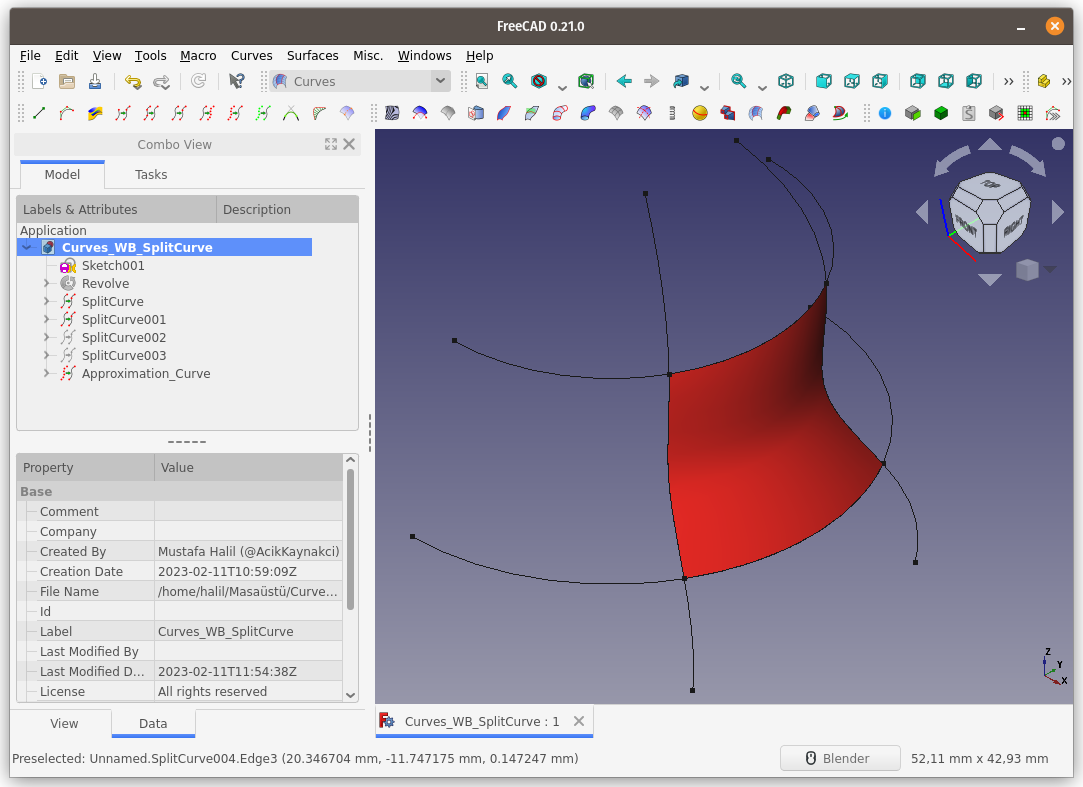
Sonuç:

<<< Curves Menü Komutlarına Ait Sayfaya Dön